На муниципальном мониторинге по математике в 9 классе, который проходил в формате ОГЭ,
На муниципальном мониторинге по математике в 9 классе, который проходил в формате ОГЭ, в одном из вариантов под номером 23 была предложена следующая задача, с которой справилось мало учащихся.
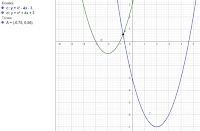
Задача.Парабола проходит через точки K(0; 2), L(–5; –3), M(1; 9). Найдите координаты её вершины.
Решение. Общий вид уравнения параболы у=ах2+bх+с. Последовательно подставляем в это уравнение координаты точек.
При подстановке координат точки K(0; 2) получаем:
2=а*02+b*0+с или с=2.
При подстановке координат точки L(–5; –3) получаем:
-3=а*(-5)2+b*(-5)+2 или 25а-5b=-5, 5a-b=-1, b=5a+1.