Графики с дыркой на ОГЭ

Рассмотрим задачи повышенной трудности из открытого банка заданий ФИПИ по математике. В них необходимо уметь строить графики различных функций, находить точки пересечения этих графиков. Такие задачи предлагаются в контрольно-измерительных материалах ОГЭ под номером 23 (модуль "Алгебра") и оцениваются в 2 балла.

Задача 1. Постройте график функции 

Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.

Решение. Определим область допустимых значений независимой переменной х (ОДЗ): x²+x≠0, x(x+1)≠0, x≠0 и x+1≠0, x≠-1.

Таким образом, х может быть любым действительным числом, кроме 0 и -1.

Теперь можем преобразовать уравнение функции:
 


 Поэтому гра­фик за­дан­ной функ­ции пред­став­ля­ет собой гиперболу

, перенесенную на 4 единицы вниз по оси у, с вы­ко­ло­той точ­кой (-1; -3).

 Пря­мая y=m не будет иметь с гра­фи­ком общих точек, если m = – 4 или m = – 3. В первом случае прямую y=- 4 ветви гиперболы не пересекают. Во втором прямая y=- 3, проходит через вы­ко­ло­тую точку графика.  

Ответ -3, -4.

Задачи для самостоятельного решения.

Задача 1. Постройте график функции 
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.

Задача 2. Постройте график функции 
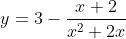
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
 Задача 3. Постройте график функции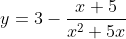 
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Задача 4. Постройте график функции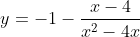 
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Задача 5. Постройте график функции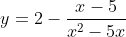 
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.