Подробно разберем решение задачи 23 из 21 варианта сборника «ОГЭ 2018. Математика. 50
вариантов. Типовые тестовые задания от разработчиков ОГЭ».
Задача. Постройте график функции у=x2–|4x+3| и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение. Рассмотрим два случая.
Первый, когда выражение под знаком модуля не отрицательно,
4x+3≥0, то есть 4x ≥-3 и x ≥-3/4. Тогда |4x+3|=4x+3 и функция принимает вид
у = x2–|4x+3| = x2–4x-3. График функции - парабола.
Второй случай, когда выражение под знаком модуля отрицательно,
4x+3<0, то есть 4x < -3 и x < -3/4.
Тогда |4x+3|= - (4x+3) = - 4x -3 и функция принимает вид
у = x2–|4x+3| = x2+4x+3. График функции - тоже парабола.
Итак график функции у=x2–|4x+3| состоит из двух парабол с общей точкой (-0,75; 0,5625) (рисунок 2).
Прямые y=m параллельны оси Ох и пересекают ось Оу в точке m. При m < -7 общих точек у прямой y=m и графика данной функции нет.
При m = -7 одна общая точка.
При -7< m < -1 две общих точки.
При m = -1 три общих точки.
При -1< m < 0,5625 четыре общих точки.
При m = 0,5625 три общих точки.
При m > 0,5625 две общих точки.
Ответ. Прямая y=m имеет с графиком ровно три общие точки при m = -1 и m = 0,5625.
Задания для самостоятельной работы.
Постройте график функции у=x2–|8x+1| и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
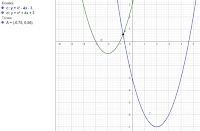 |
| Рис 1. 2 параболы |
Решение. Рассмотрим два случая.
Первый, когда выражение под знаком модуля не отрицательно,
4x+3≥0, то есть 4x ≥-3 и x ≥-3/4. Тогда |4x+3|=4x+3 и функция принимает вид
у = x2–|4x+3| = x2–4x-3. График функции - парабола.
Второй случай, когда выражение под знаком модуля отрицательно,
4x+3<0, то есть 4x < -3 и x < -3/4.
Тогда |4x+3|= - (4x+3) = - 4x -3 и функция принимает вид
 |
| Рис 2. График функции у=x2–|4x+3| |
Итак график функции у=x2–|4x+3| состоит из двух парабол с общей точкой (-0,75; 0,5625) (рисунок 2).
Прямые y=m параллельны оси Ох и пересекают ось Оу в точке m. При m < -7 общих точек у прямой y=m и графика данной функции нет.
При m = -7 одна общая точка.
При -7< m < -1 две общих точки.
При m = -1 три общих точки.
При -1< m < 0,5625 четыре общих точки.
При m = 0,5625 три общих точки.
При m > 0,5625 две общих точки.
Ответ. Прямая y=m имеет с графиком ровно три общие точки при m = -1 и m = 0,5625.
 |
| При m = -7 одна общая точка |
 |
| При -7< m < -1 две общих точки |
 |
| При m = -1 три общих точки |
 |
| При -1< m < 0,5625 четыре общих точки |
 |
| При m = 0,5625 три общих точки |
 |
| При m > 0,5625 две общих точки |
Задания для самостоятельной работы.
Постройте график функции у=x2–|8x+1| и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Комментариев нет:
Отправить комментарий