Вспомним, что любая прямая на координатной плоскости может быть задана уравнением y = kx + b, где k - некоторое число, называемое угловым коэффициентом прямой, b – некоторое число.
Далее, вспомним, что все прямые с одним и тем же
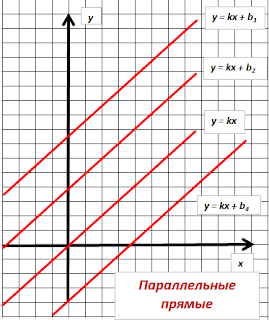
угловым коэффициентом параллельны. Если b =0, то прямая проходит через начало координат. На
рисунке справа изображены четыре параллельные прямые с угловым коэффициентом k, одна из них y = kx проходит через начало координат.
Например, на следующем графике приведены четыре
прямые с угловым коэффициентом k = 2 :
y = 2x + 12,
y = 2x + 4,
y = 2x,
y = 2x – 4.
Углом
наклона прямой
y = kx+b называют угол a, отсчитываемый от положительного
направления оси абсцисс до прямой y = kx+b в положительном направлении
(то есть, против часовой стрелки).
Угловой
коэффициент прямой равен тангенсу угла наклона прямой, то есть, k = tgα .
На рисунке прямая y = 2x + 12 образует с осью абсцисс угол ВАО, а прямая y = 2x угол КОС. Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Из треугольника АВО находим tgВАО = ВО:АО = 12:6 = 2. Из треугольника КОС находим tgКОС = КС:ОС = 8:4 = 2. Мы ещё раз проверили, что угловые коэффициенты у параллельных прямых равны.
Теперь
рассмотрим все возможные случаи. Угол наклона прямой равен нулю, когда прямая
параллельна оси абсцисс. В этом случае нулю равен и угловой коэффициент, так
как тангенс нуля есть ноль. Следовательно, уравнение прямой будет иметь вид y
= b. На рисунке красным цветом изображены прямые y = 5, y = 1, y = -3.
В случае,
когда α = 90° прямая
располагается перпендикулярно оси абсцисс (параллельно оси ординат) и задается
равенством x = c, где c - некоторое действительное число. На
рисунке голубым цветом изображены прямые х = 3, х = -3.
Когда угол
наклона прямой y = kx+b является острым ( 0°< α <90°), то угловой коэффициент k является
положительным числом (так как тангенс острого угла α принимает положительные значения tgα>0) и
указывает на возрастание графика прямой.
Когда угол наклона прямой y = kx+b является тупым (90°< α < 180° ), то угловой коэффициент k является отрицательным числом и указывает на убывание графика прямой. Это вытекает из того, что тангенс тупого угла отрицателен. Для нахождения тангенса угла наклона в этом случае необходимо использовать формулу tg(180° – α) = - tgα. Поэтому на рисунке мы найдём тангенс угла АВО, tgАВО = АО:ОВ =6:8 = 0,75. Значит угловой коэффициент прямой k = tgα = - 0,75.
Касательной к графику функции y = f(x) в точке х0 называют прямую, проходящую через точку (х0, f(x0)), причём эта точка единственная общая точка функции и прямой в некоторой окрестности данной точки. На рисунке прямая y = kx+b касается графика функции y = f(x) в точке х0.
Геометрический
смысл производной заключается в том, что значение производной функции
y = f(x) в точке х0 равно
тангенсу угла наклона касательной l, проведённой к графику данной функции в точке с абсциссой х0, то есть k = tgα = f'(x0) - угловой коэффициент прямой l.
Уравнение касательной прямой.
Для
записи уравнения любой прямой на плоскости достаточно знать ее угловой
коэффициент и точку, через которую она проходит. Касательная прямая проходит
через точку касания и ее угловой коэффициент для дифференцируемой функции равен
значению производной в точке x0. То есть, из геометрического смысла производной функции в точке мы можем взять все данные для записи уравнения
касательной прямой.
Уравнение касательной к графику функции y = f(x)
в точке x0 имеет вид
y = f'(x0)(х – х0) + f(x0)
Рассмотрим примеры из открытого банка заданий по математике ЕГЭ 2013. Сайт mathege.ru.
Задание B8 (№ 6007)
Прямая у = 7х - 5 параллельна касательной к графику функции у = х2 + 6х - 8. Найдите абсциссу точки касания.
Решение. Поскольку
касательная параллельна прямой у = 7х – 5, значит её угловой коэффициент
равен 7. По геометрическому смыслу производной k = f'(x0). Таким образом, чтобы найти абсциссу точки
касания, мы должны найти производную функции и приравнять её к 7.
Находим
производную: у' = (х2 + 6х – 8)'
= 2х + 6.
Приравниваем
к 7, получаем 2х + 6= 7, 2х = 1, х = 0,5.
Таким образом мы нашли, что касательная к графику функции у = х2
+ 6х – 8, проведённая в точке х = 0,5, будет параллельна прямой у = 7х – 5.
Ответ 0,5.
Аналогично
решаются следующие задания, тренируйтесь.
Задание B8 (№ 6009)
Прямая у = 6х + 8 параллельна касательной
к графику функции у = х2 - 3х +
5. Найдите абсциссу точки касания.
Ответ 4,5.
Задание B8 (№ 6011)
Прямая у = 7х + 11 параллельна касательной
к графику функции у = х2 + 8х +
6 . Найдите абсциссу точки касания.
Ответ -0,5.
Задание B8 (№ 6013)
Прямая у = 4х + 8 параллельна касательной
к графику функции у = х2 - 5х +
7
.
Найдите абсциссу точки касания.
Ответ 4,5.
Задание B8 (№ 6015)
Прямая у = 3х + 6 параллельна касательной
к графику функции у = х2 - 5х +
8. Найдите абсциссу точки касания.
Ответ 4.
(продолжение следует)





Комментариев нет:
Отправить комментарий